Answer:
Point C: (3, 3)
Point D: (3, -22)
Explanation:
If the distance between points C and D is 25 units, the y-value of point D will be 25 less than the y-value of point C. The x-values of the two points are the same.
Therefore:

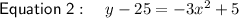
As the x-values are the same, substitute the first equation into the second equation and solve for x to find the x-value of points C and D:
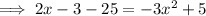
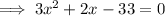
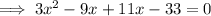


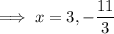
From inspection of the given graph, the x-value of points C and D is positive, therefore x = 3.
To find the y-value of points C and D, substitute the found value of x into the two original equations of the lines:
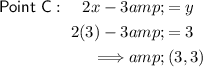
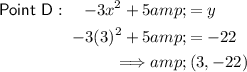
Therefore, point C is (3, 3) and point D is (3, -22).