Answer:
The plane's resultant vector is 890.3 miles, at an angle of 59.5° west of north.
Explanation:
• To find the magnitude of the resultant vector, we have to use Pythagoras's theorem:
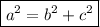
where:
a ⇒ hypotenuse (= resultant vector = ? mi)
b, c ⇒ the two other sides of the right-angled triangle (= 452 mil North, 767 mi West).
Using the formula:
resultant² =
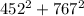
⇒ resultant =
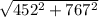
⇒ resultant = 890.3 mi
• To find the direction, we can find the angle (labeled x in diagram) that the resultant makes with the north direction:
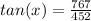
⇒
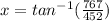
⇒
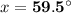
∴ The plane's resultant vector is 890.3 miles, at an angle of 59.5° west of north .