Question

A plane flies 452 miles north and then 767 miles west. What is the magnitude and direction of the plane's resultant vector?

Answer 1

`\displaystyle Approximately\:59°\:at\:a\:magnitude\:of\:approximately\:890\:miles`

Explanation:

`\displaystyle (OPPOCITE)/(HYPOTENUSE) = sin\:\theta \\ (ADJACENT)/(HYPOTENUSE) = cos\:\theta \\ (OPPOCITE)/(ADJACENT) = tan\:\theta \\ (HYPOTENUSE)/(ADJACENT) = sec\:\theta \\ (HYPOTENUSE)/(OPPOCITE) = csc\:\theta \\ (ADJACENT)/(OPPOCITE) = cot\:\theta`

We must use trigonometry to help us find the direction of the aeroplane's resultant vector. Do as I do:

`\displaystyle (452)/(767) = cot\:x \hookrightarrow cot^(-1)\:(452)/(767) = x; 59,488772482...° = x \\ \\ \boxed{59° \approx x}`

Now, we will use the Pythagorean Theorem to find the magnitude of the aeroplane's resultant vector. Do as I do:

`\displaystyle a^2 + b^2 = c^2 \\ \\ 767^2 + 452^2 = c^2 \\ √(792593) = √(c^2); 890,27692321... = c \\ \\ \boxed{890 \approx c}`

Therefore, the direction and magnitude of the aeroplane's resultant vector are approximately eight hundred ninety miles at an angle of elevation of fifty-nine degrees.

I am joyous to assist you at any time.

Answer 2

The plane's resultant vector is 890.3 miles, at an angle of 59.5° west of north.

Explanation:

• To find the magnitude of the resultant vector, we have to use Pythagoras's theorem:

`\boxed{a^2 = b^2 + c^2}`

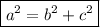
where:

a ⇒ hypotenuse (= resultant vector = ? mi)

b, c ⇒ the two other sides of the right-angled triangle (= 452 mil North, 767 mi West).

Using the formula:

resultant² =
`452^2 + 767^2`

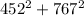
⇒ resultant =
`√(452^2 + 767^2)`

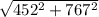
⇒ resultant = 890.3 mi

• To find the direction, we can find the angle (labeled x in diagram) that the resultant makes with the north direction:

`tan (x) =(767)/(452)`

⇒
`x = tan^(-1) ((767)/(452) )`

⇒
`x = \bf{59.5 \textdegree}`

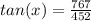
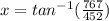
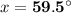
∴ The plane's resultant vector is 890.3 miles, at an angle of 59.5° west of north .