Question

One method for estimating the availability of office space in large cities is to conduct arandom sample of offices, and calculate the proportion of offices currently being used. Suppose that realestate agents believe that p = 0.70 of all offices are currently occupied, and decide to take a sample toassess their belief. They are considering a sample size of n = 40.a)

a. Show that this sample size is large enough to justify using the normal approximation to thesampling distribution of p.
b. What is the mean of the sampling distribution of p if the real estate agents are correct?
c. What is the standard deviation of the sampling distribution of p if the real estate agents arecorrect?
d. If the real estate agents are correct, what is the probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05?

Answer 1

The sample size of 40 is large enough to justify using the normal approximation. The mean of the sampling distribution of p is 0.70. The standard deviation of the sampling distribution of p is approximately 0.095.

Step-by-step explanation:

To determine whether the sample size is large enough to justify using the normal approximation to the sampling distribution of p, we need to check if both np and n(1-p) are greater than 10. In this case, p is 0.70 and n is 40. So, np = 40(0.70) = 28 and n(1-p) = 40(0.30) = 12, which are both greater than 10. Therefore, the sample size is large enough to use the normal approximation.

The mean of the sampling distribution of p is equal to p itself. In this case, if the real estate agents are correct, the mean would be 0.70.

The standard deviation of the sampling distribution of p can be calculated using the formula: sqrt((p(1-p))/n). Plugging in the values, we get sqrt((0.70(1-0.70))/40) = sqrt(0.21/40) ≈ 0.095.

If the real estate agents are correct and p is 0.70, we can use the normal distribution to find the probability that a sample proportion, p, would differ from 0.70 by as much as 0.05. We can calculate the z-score using the formula (p - p') / sqrt((p(1-p))/n). Plugging in the values, we get (0.75 - 0.70) / sqrt((0.70(1-0.70))/40) ≈ 0.05 / 0.095 ≈ 0.526. By looking up the z-score in the standard normal distribution table, we can find the probability that corresponds to it.

Answer 2

a) Since np >= 5 and n(1-p) >= 5, the approximation is justified

b) 0.7

c) 0.0725

d) 0.5098 = 50.98% probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05

Step-by-step explanation:

We use the normal distribution and the central limit theorem to solve this question.

Normal probability distribution

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central Limit Theorem

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
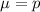`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

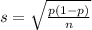
In this question, we have that:

`p = 0.7, n = 40`

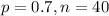
a. Show that this sample size is large enough to justify using the normal approximation to thesampling distribution of p.

We need that: np >= 5, n(1-p) >= 5. So

np = 40*0.7 = 28 > 5

n(1-p) = 40*0.3 = 12 > 5

Since both conditions are satisfied, the approximation is justified.

b. What is the mean of the sampling distribution of p if the real estate agents are correct?

This is
`\mu = p = 0.7`

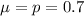
c. What is the standard deviation of the sampling distribution of p if the real estate agents are correct?

This is
`s = \sqrt{(p(1-p))/(n)} = \sqrt{(0.7*0.3)/(40)} = 0.0725`

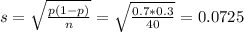
d. If the real estate agents are correct, what is the probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05?

This is the pvalue of Z when X = 0.7 + 0.05 = 0.75 subtracted by the pvalue of Z when X = 0.7 - 0.05 = 0.65. So

X = 0.75

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (0.75 - 0.7)/(0.0725)`

`Z = 0.69`

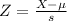
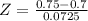
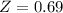
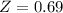`Z = 0.69` has a pvalue of 0.7549

X = 0.65

`Z = (X - \mu)/(s)`

`Z = (0.65 - 0.7)/(0.0725)`

`Z = -0.69`

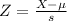
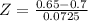
`Z = -0.69` has a pvalue of 0.2451

0.7549 - 0.2451 = 0.5098

0.5098 = 50.98% probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05