Answer:
a) Since np >= 5 and n(1-p) >= 5, the approximation is justified
b) 0.7
c) 0.0725
d) 0.5098 = 50.98% probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05
Step-by-step explanation:
We use the normal distribution and the central limit theorem to solve this question.
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
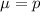 and standard deviation
and standard deviation
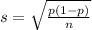
In this question, we have that:
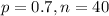
a. Show that this sample size is large enough to justify using the normal approximation to thesampling distribution of p.
We need that: np >= 5, n(1-p) >= 5. So
np = 40*0.7 = 28 > 5
n(1-p) = 40*0.3 = 12 > 5
Since both conditions are satisfied, the approximation is justified.
b. What is the mean of the sampling distribution of p if the real estate agents are correct?
This is
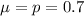
c. What is the standard deviation of the sampling distribution of p if the real estate agents are correct?
This is
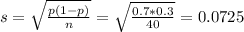
d. If the real estate agents are correct, what is the probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05?
This is the pvalue of Z when X = 0.7 + 0.05 = 0.75 subtracted by the pvalue of Z when X = 0.7 - 0.05 = 0.65. So
X = 0.75

By the Central Limit Theorem
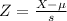
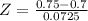
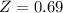
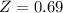 has a pvalue of 0.7549
has a pvalue of 0.7549
X = 0.65
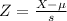
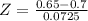

 has a pvalue of 0.2451
has a pvalue of 0.2451
0.7549 - 0.2451 = 0.5098
0.5098 = 50.98% probability that a sample proportion, p,would differ from p = 0.70 by as much as 0.05