Question

A landscaper is designing a flower garden in the shape of a trapezoid. She wants the shorter base to be 3 yards greater than the height and the longer base to be 7 yards greater than the height. She wants the area to be 295 square yards. The situation is modeled by the equation h^2 + 5h = 295. Use the Quadratic Formula to find the height that will give the desired area. Round to the nearest hundredth of a yard.

A: 17.36 yards
B: 600 yards
C: 14.86 yards
D: 29.71 yards

Answer 1

C: 14.86 yards

Explanation:

to solve a quadratic equation we need to make it equal to zero and then use the Quadratic Formula

`x= \frac{-b + \sqrt{b^(2)-4ac}}{2a}​​ / \frac{-b - \sqrt{b^(2)-4ac}}{2a}​​`

having

`h^(2) +5h-295=0`

we have

a=1

b=5

c=-295

​​the answers for the formula are

h=14.85 and h=-17.36

as we are looking for a distance we can only take the positive answer, then

h=14.85

Answer 2

The height is 14.86 yards ⇒ answer C

Explanation:

* Lets explain how to solve the problem

- The flower garden in the shape of a trapezoid

- The shorter base to be 3 yards greater than the height

- The longer base to be 7 yards greater than the height

- The area must be 295 square yards

- The situation is modeled by the equation h² + 5h = 295

- We want to find the height that will give the desired area by using

the quadratic formula

- The quadratic formula is
`h=\frac{-b+-\sqrt{b^(2)-4ac}}{2a}`,

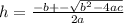where a is the coefficient of h² and b is the coefficient of h and c

is the numerical term

- The equation of the area is h² + 5h = 295

∵ h² + 5h = 295

- Subtract 295 from both sides

∴ h² + 5h - 295 = 0

- Lets find the values of a , b and c from the equation

∵ a = 1 , b = 5 , c = -295

∴
`h=\frac{-5+-\sqrt{(5)^(2)-4(1)(-295)}}{2(1)}`

∴
`h=(-5+-√(25+1180))/(2)`

∴
`h=(-5+√(1205))/(2)=14.86`

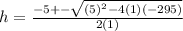
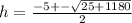
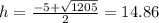
- OR

∴
`h=(-5-√(1205))/(2)=-19.86`

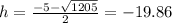
- The dimensions of any figure must be positive value, then we will

neglect the negative value of h

∴ h = 14.86

* The height is 14.86 yards