Question

Phosphorus-32 has a half-life of 14.0 days. Starting with 4.00 g of 32P, how many grams will remain after 84.0 days ?

Answer 1

t₁=84 d
t₂=14 d
m₁=4 g

n=t₁/t₂
n=84/14=6

m₂=m₁/2ⁿ

m₂=4/(2⁶)=0.0625 g

0.0625 grams will remain after 84.0 days

Answer 2

Answer: The final amount will be 0.0625 grams.

Solution: Radioactive decay obeys first order kinetics and the first order integrated rate law equation is:

`ln(A)=-kt+ln(A_0)`

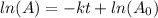
where,
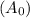`(A_0)` is the initial amount and A is the final amount, k is the decay constant and t is the time.

First of all we calculate the decay constant from given half life using the equation:

`k=(0.693)/(halfLife)`

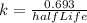
Given half life is 14.0 days,

So,
`k=(0.693)/(14.0days)`

`k=0.0495days^-^1`

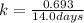
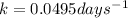
Initial amount is given as 4.00 g and the time is 84.0 days. Let's plug in the values in the first order integrated rate law equation and calculate the final amount.

`ln(A)=-0.0495days^-^1(84.0days)+ln(4.00)`

`ln(A)=-4.158+1.386`

`ln(A)=-2.772`

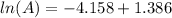
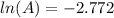
taking anti ln to both sides:

`A=e^-^2^.^7^7^2`

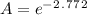
A = 0.0625

So, the remaining amount after 84.0 days will be 0.0625 grams.