Answer: The final amount will be 0.0625 grams.
Solution: Radioactive decay obeys first order kinetics and the first order integrated rate law equation is:
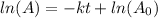
where,
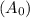 is the initial amount and A is the final amount, k is the decay constant and t is the time.
is the initial amount and A is the final amount, k is the decay constant and t is the time.
First of all we calculate the decay constant from given half life using the equation:
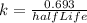
Given half life is 14.0 days,
So,
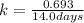
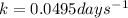
Initial amount is given as 4.00 g and the time is 84.0 days. Let's plug in the values in the first order integrated rate law equation and calculate the final amount.
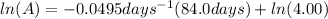
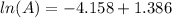
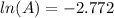
taking anti ln to both sides:
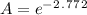
A = 0.0625
So, the remaining amount after 84.0 days will be 0.0625 grams.