Answer:

Explanation:
Given: The probability that a fish eats shrimp only =
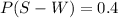
The probability that a fish eats shrimp and worms =
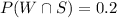
Now, the probability that a fish eats shrimp =
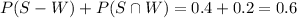
The probability that a fish eats worms, given that it eats shrimp is given by:-
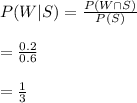
The probability that a fish eats worms, given that it eats shrimp=
