Question

Explain how to do this problem:

Xavier determined that some fish like to eat worms, some like to eat shrimp, and others don't like to eat worms or shrimp. He calculated the probabilities and created the Venn diagram below:

a venn diagram showing two categories, worms and shrimp. In the worms only circle is 0.3, in the shrimp only circle is 0.4, in the intersection is 0.2, outside the circles is 0.1

What is the probability that a fish eats worms, given that it eats shrimp?

Answer 1

Answer:
`(1)/(3)`

Explanation:

Given: The probability that a fish eats shrimp only =
`P(S-W)=0.4`

The probability that a fish eats shrimp and worms =
`P(W\cap S)=0.2`

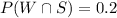
Now, the probability that a fish eats shrimp =
`P(S-W)+P(S\cap W)=0.4+0.2=0.6`

The probability that a fish eats worms, given that it eats shrimp is given by:-

`P(W|S)=(P(W\cap S))/(P(S))\\\\=(0.2)/(0.6)\\\\=(1)/(3)`

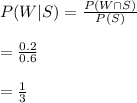
The probability that a fish eats worms, given that it eats shrimp=
`(1)/(3)`

Answer 2

Probability of a fish eat worms given that it eats shrimp


`P(w|s)= (P(w∩s)/(P(s))`

`P(w|s)= (0.2)/(0.6)`

`P(w|s)= (1)/(3)`