The energy of electromagnetic waves can be calculated by using the following formula:
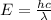
where:
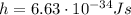 is the Planck constant
is the Planck constant
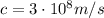 is the speed of light
is the speed of light
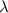 is the wavelength of the wave
is the wavelength of the wave
Substituting the various wavelengths in the formula, we find:
IR-C:
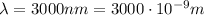 -->
-->
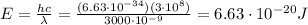
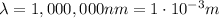 -->
-->
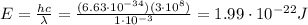
IR-A:
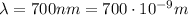 -->
-->
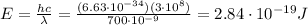
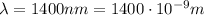 -->
-->
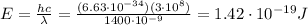
Therefore, we see that IR-A have higher energy than IR-C.