Question

Two of the types of infrared light, ir-c and ir-a, are both components of sunlight. their wavelengths range from 3000 to 1,000,000 nm for ir-c and from 700 to 1400 nm for ir-

a. compare the energy of microwaves, ir-c, and ir-
a.

Answer 1

The energy of electromagnetic waves can be calculated by using the following formula:

`E=(hc)/(\lambda)`

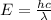
where:

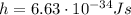`h=6.63 \cdot 10^(-34) Js` is the Planck constant

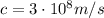`c=3\cdot 10^8 m/s` is the speed of light

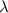`\lambda` is the wavelength of the wave

Substituting the various wavelengths in the formula, we find:

IR-C:

`\lambda=3000 nm=3000\cdot 10^(-9) m` -->

`E=(hc)/(\lambda)=((6.63 \cdot 10^(-34))(3 \cdot 10^8))/(3000\cdot 10^(-9))=6.63 \cdot 10^(-20) J`

`\lambda=1,000,000 nm=1\cdot 10^(-3) m` -->

`E=(hc)/(\lambda)=((6.63 \cdot 10^(-34))(3 \cdot 10^8))/(1\cdot 10^(-3))=1.99 \cdot 10^(-22) J`

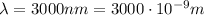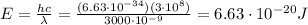
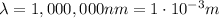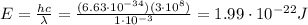
IR-A:

`\lambda=700 nm=700\cdot 10^(-9) m` -->

`E=(hc)/(\lambda)=((6.63 \cdot 10^(-34))(3 \cdot 10^8))/(700\cdot 10^(-9))=2.84 \cdot 10^(-19) J`

`\lambda=1400 nm=1400\cdot 10^(-9) m` -->

`E=(hc)/(\lambda)=((6.63 \cdot 10^(-34))(3 \cdot 10^8))/(1400\cdot 10^(-9))=1.42 \cdot 10^(-19) J`

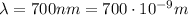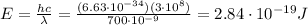
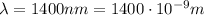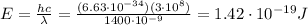
Therefore, we see that IR-A have higher energy than IR-C.

Answer 2

The energy of a light wave is calculated using the formula
E = hc/λ
h is the Planck's constant
c is the speed of light
λ is the wavelength
For the ir-c, the range is
6.63 x 10^-34 (3x10^8) / 3000 = 6.63 x 10 ^-29 J
6.63 x 10^-34 (3x10^8) / 1000000 = 1.99 x 10^-31 J

For the ir-a, the range is
6.63 x 10^-34 (3x10^8) / 700 = 2.84 x 10^-28 J
6.63 x 10^-34 (3x10^8) / 1400 = 1.42 x 10^-28 J