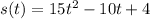Question

An object has a constant acceleration of 30 ft/sec2, an initial velocity of -10 ft/sec, and an initial position of 4 ft. Find the position function, s(t), describing the motion of the object.

Answer 1

x(t)=15t^2 - 10t + 4

Explanation:

As we know the equation of motion is x(t) = (1/2)a t^2 +vi + xi

where a is acceleration, vi is initial velocity and xi is initial position

For t in seconds and x(t) in feet, your values make this equation be

x(t)=15t^2 - 10t + 4

Answer 2

Let
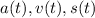
`a(t),v(t),s(t)` be the acceleration, velocity, and position functions, respectively. Then


`v(t)=s'(t)`

`a(t)=v'(t)=s''(t)`

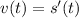
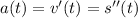
Since the acceleration is a constant 30 ft/s^2, you have


`a(t)=s''(t)=30`

`\displaystyle\int s''(t)\,\mathrm dt=\int30\,\mathrm dt`

`\displaystyle s'(t)=v(t)=30t+C_1`

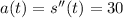
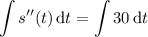
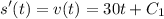
You're told that the initial velocity is
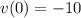
`v(0)=-10`, so you get


`-10=30(0)+C_1\implies C_1=-10`

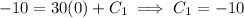
Now
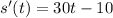
`s'(t)=30t-10`. Integrating once more, you find


`\displaystyle\int s'(t)\,\mathrm dt=\int(30t-10)\,\mathrm dt`

`s(t)=15t^2-10t+C_2`

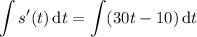
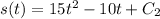
and since
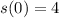
`s(0)=4`, you get


`4=15(0)^2-10(0)+C_2\implies C_2=4`

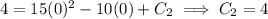
which means the exact position function is


`s(t)=15t^2-10t+4`