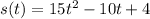Let

be the acceleration, velocity, and position functions, respectively. Then
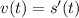
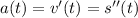
Since the acceleration is a constant 30 ft/s^2, you have


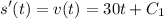
You're told that the initial velocity is
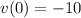
, so you get
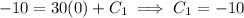
Now
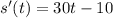
. Integrating once more, you find
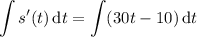
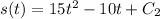
and since
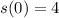
, you get
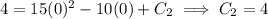
which means the exact position function is