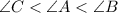Question

The perimeter of ABC is 30 feet. AB=5x-7, BC=3x+1, AC=4x. List the angles of ABC in order from smallest to largest

A) Angle A, B, C
B) Angle A, C, B
C) Angle C, B, A
D) Angle C, A, B

Answer 1

lets say we have a triangle ABC
if A is the biggest angle, the side oposite that angle (BC) will be the longest
so

perimiter=AB+BC+AC
P=30=5x-7+3x+1+4x
find x
30=5x-7+3x+1+4x
30=5x+3x+4x-7+1
30=12x-6
add 6
36=12x
divide 12
3=x


evaluate each
AB=5(3)-7=15-7=22
BC=3(3)+1=9+1=10
AC=4(3)=12

AB>AC>BC
the oposite one
C>B>A
smallest to largest
A<B<C
answer is option A

Answer 2

Option D is correct.

From smallest to largest the angles are; Angles C , A , B

Explanation:

Perimeter of a triangle is the sum of all the sides.

Given: In triangle ABC, the perimeter is 30 feet and

AB = 5x -7 , BC = 3x+1 and AC =4x

By definition of perimeter;

Perimeter of triangle ABC = AB + BC + AC

Substitute given values we have;

`30 = 5x -7 + 3x +1 +4x`

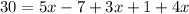
Combine like terms;

`30 = 12x - 6`

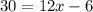
Add 6 to both sides we get;

30 +6 = 12x -6 +6

Simplify:

36 = 12 x

Divide both sides by 12 we get;

3 = x

Side of AB = 5x -7 = 5(3) -7 = 15 -7 = 8 units.

Side of BC = 3x + 1 = 3(3) + 1 = 9 + 1 = 10 units.

and

Side of AC = 4x = 4(3) = 12 units.

`AB < BC < AC`

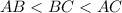
As, the largest angle will be opposite 12 because it is the longest side. Similarly, the smallest angle will be opposite 8, which is the shortest side.

`\angle C < \angle A < \angle B`