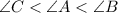Answer:
Option D is correct.
From smallest to largest the angles are; Angles C , A , B
Explanation:
Perimeter of a triangle is the sum of all the sides.
Given: In triangle ABC, the perimeter is 30 feet and
AB = 5x -7 , BC = 3x+1 and AC =4x
By definition of perimeter;
Perimeter of triangle ABC = AB + BC + AC
Substitute given values we have;
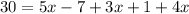
Combine like terms;
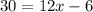
Add 6 to both sides we get;
30 +6 = 12x -6 +6
Simplify:
36 = 12 x
Divide both sides by 12 we get;
3 = x
Side of AB = 5x -7 = 5(3) -7 = 15 -7 = 8 units.
Side of BC = 3x + 1 = 3(3) + 1 = 9 + 1 = 10 units.
and
Side of AC = 4x = 4(3) = 12 units.

As, the largest angle will be opposite 12 because it is the longest side. Similarly, the smallest angle will be opposite 8, which is the shortest side.