Question

Write the equation of the parabola that has the vertex at point (2,7) and passes through the point (−1,3).

Answer 1

U add the X and Ys to get a new point

Answer 2

Given, the vertex of a parabola is (2,7).

We know the the general equation of vertex form of parabola is

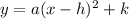`y = a(x-h)^2+k`, where (h,k) is the vertex of the parabola.

Here the value of h = 2, k = 7. So by substituting the values of h and k in the general equation we will get,

`y = a(x-2)^2+7`

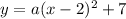
Given the parabola passes through the point (-1,3). So we will substitute x = -1 and y = 3 in this equation to find a. We will get,

`3 = a(-1-2)^2+7`

`3 = a(-3)^2+7`

`3 = a(9) +7`

`3 = 9a+7`

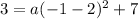
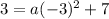
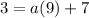
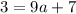
Now we can get a by moving 7 to the left side by subtracting it from both sides. We will get,

`3-7 = 9a+7-7`

`-4 = 9a`

`9a = -4`

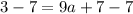
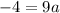
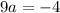
Now to get a we will move 9 to the right side by dividing it to both sides. We will get,

`(9a)/(9) =((-4))/(9)`

`a = -(4)/(9)`

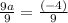
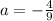
So the equation of the parabola is,

`y =-(4)/(9) (x-2)^2+7`

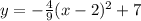
To simplify the equation we will multiply both sides by 9. We will get,

`9y = (9)(-(4)/(9)(x-2)^2+7))`

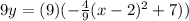
When we distribute 9 to the right side we will get,

`9y = -4(x-2)^2+63`

`9y = -4(x^2-4x+4)+63`

`9y = -4x^2+16x-16+63`

`9y = -4x^2+16x+47`

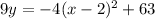
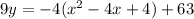
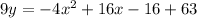
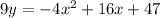
So we have got the required equation of parabola.