Given, the vertex of a parabola is (2,7).
We know the the general equation of vertex form of parabola is
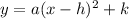 , where (h,k) is the vertex of the parabola.
, where (h,k) is the vertex of the parabola.
Here the value of h = 2, k = 7. So by substituting the values of h and k in the general equation we will get,
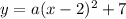
Given the parabola passes through the point (-1,3). So we will substitute x = -1 and y = 3 in this equation to find a. We will get,

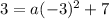
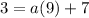
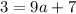
Now we can get a by moving 7 to the left side by subtracting it from both sides. We will get,
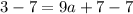
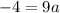
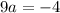
Now to get a we will move 9 to the right side by dividing it to both sides. We will get,
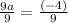
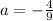
So the equation of the parabola is,

To simplify the equation we will multiply both sides by 9. We will get,
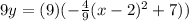
When we distribute 9 to the right side we will get,
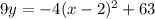
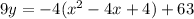
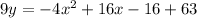
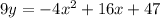
So we have got the required equation of parabola.