Answer:
B. 0.0611
Explanation:
We have been given that a data set which follows a nonstandard normal distribution curve and mean of data set is 715 and standard deviation is 24.
To find the probability that a randomly selected value will be between 660 and 680 we will use probability formula to find the values between two z-scores.
First of all let us find z-score for our given values using z-score formula.
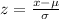 , where,
, where,
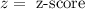 ,
,
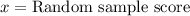 ,
,
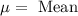 ,
,
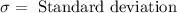 .
.
Let us find z-score for random score 660.

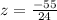
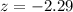
Let us find z-score for random score 680.
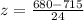
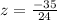

We will use formula
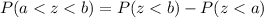 to find the probability between our given values.
to find the probability between our given values.
Upon substituting our given values in above formula we will get,
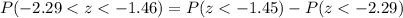
Using normal distribution table we will get,
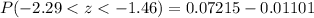

Therefore, the probability that a randomly selected value will be between 660 and 680 is 0.0611 and option B is the correct choice.