Question

A set of data follows a nonstandard normal distribution curve. Find the probability that a randomly selected value will be between 660 and 680 given mean of 715 and a standard deviation of 24

Options:
0.9169
0.0611
0.7100
0.8300

Answer 1

0.0611

Explanation:

Answer 2

B. 0.0611

Explanation:

We have been given that a data set which follows a nonstandard normal distribution curve and mean of data set is 715 and standard deviation is 24.

To find the probability that a randomly selected value will be between 660 and 680 we will use probability formula to find the values between two z-scores.

First of all let us find z-score for our given values using z-score formula.

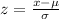`z=(x-\mu)/(\sigma)`, where,

`z=\text{ z-score}`,

`x=\text{Random sample score}`,

`\mu=\text{ Mean}`,

`\sigma=\text{ Standard deviation}`.

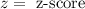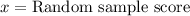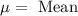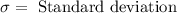Let us find z-score for random score 660.

`z=(660-715)/(24)`

`z=(-55)/(24)`

`z=-2.29`

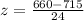
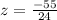
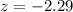
Let us find z-score for random score 680.

`z=(680-715)/(24)`

`z=(-35)/(24)`

`z=-1.458\approx -1.46`

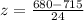
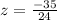
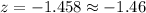
We will use formula
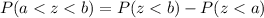`P(a<z<b)=P(z<b)-P(z<a)` to find the probability between our given values.

Upon substituting our given values in above formula we will get,

`P(-2.29<z<-1.46)=P(z<-1.45)-P(z<-2.29)`

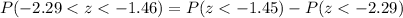
Using normal distribution table we will get,

`P(-2.29<z<-1.46)=0.07215-0.01101`

`P(-2.29<z<-1.46)=0.06114`

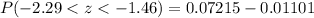
Therefore, the probability that a randomly selected value will be between 660 and 680 is 0.0611 and option B is the correct choice.