***The complete question is: Let f(x)= sqrt 6x and g(x)=x+3 smallest number that is in the domain of f(g(x))***
Answer: The smallest number that is in the domain is -3.
Step-by-step explanation:
Given functions:
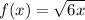
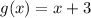
To find f(g(x)), put g(x) in f(x) as follows:
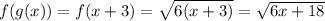
As (6x+18) is in square-root (and square-root of a negative number is an imaginary value), therefore, the domain should be the following:
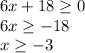
Therefore, the domain is [-3, +∞).
So the smallest number that is in the domain is -3.