Answer:
Option 2 is correct.
The axis of symmetry is, x= 3
Explanation:
Given: The zeros of the quadratic function f are 1 and 5.
If the zeroes are at x =1 and at x =5, then,
the factor equations were x- 1=0 and x-5 = 0.
Then. the factors were x -1 and x-5 .
Any factorable quadratic is going to have just the two factors, so these are must be them.
Then, the original quadratic was :
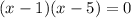
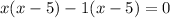 or
or
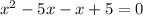 [by distributive property
[by distributive property
 ]
]
Combine like terms;
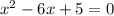 ......[1]
......[1]
A quadratic equation is of the form:
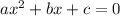 ; where a, b, c are the coefficient ]
; where a, b, c are the coefficient ]
On comparing equation [1] with general equation we have;
the value of a = 1 , b = -6 and c =5
Axis of symmetry states that a parabola is a vertical line that divides the parabola into two congruent halves.
i,e
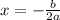
Then;
Axis of symmetry (x) =
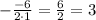
Therefore, the equation of the axis of symmetry is; x = 3