Question

Find the x-coordinates of any relative extrema and inflection point(s) for the function f of x equals 9 times x raised to the one third power plus 9 halves times x raised to the four thirds power . You must justify your answer using an analysis of f ?(x) and f ??(x).

Answer 1

f(x) = 9x∧1/3 + 91/2x∧4/3

Step-by-step explanation: y=f(x)

∴ y = 9x∧1/3 + 91/2x4/3

dy/dx = {9x∧-2/3}/3 + {36x∧1/3}/3

dy/dx = 3/x∧2/3 + 12x∧1/3 = 3/∧x2/3{ 1 + 4x}

For, 1 +4x = 0

4x = -1

∴ x = -1/4

Inflection point, x = -1/4

Answer 2

reletive extrema are where the first derivitive is 0 and the sign of the first derivitive changes

inflection points are where the 2nd derivitive is 0 and the sign of the 2nd derivitive changesd

I use f'(x)=1st derivitive and f''(x)=2nd derivitive

remember power rule:
`(d)/(dx) x^m=mx^(m-1)`

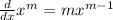
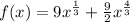
`f(x)=9x^(1)/(3)+(9)/(2)x^(4)/(3)`

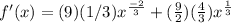
f'(x)

`f'(x)=(9)(1/3)x^(-2)/(3)+((9)/(2))((4)/(3))x^(1)/(3)`

`f'(x)=3x^(-2)/(3)+6x^(1)/(3)`

f''(x)

`f''(x)=(3)((-2)/(3))x^(-5)/(3)+(6)((1)/(3))x^(-2)/(3)`

`f''(x)=-2x^(-5)/(3)+2x^(-2)/(3)`

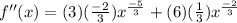
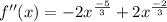
I'm not going to show the work for solving for when f'(x)=0 and f''(x)=0 because at this stage of the game, you should be able to do that easily

f'(x) is equal to 0 when x=-0.5, the sign changes from negative to positive at this point so at this point, the function has a relative minimum

f''(x) is equal to 0 when x=1, the sign changes from negative to positive at this point so at this point, the function is changing from concave down to concave up