Answer:
Options 1 and 3.
Explanation:
By definition the product between two matrices is:
Let's suppose both matrices are 2x2,
![A=\left[\begin{array}{cc}a_(11)&a_(12)\\a_(21)&a_(22)\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/yhn9qvgsg0fzank20pbhr26s9rpaigrtjs.png)
![B=\left[\begin{array}{cc}b_(11)&b_(12)\\b_(21)&b_(22)\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/i8xdxrhk428etoupw86c52t1dz6try6qpu.png)
The product between A and B is:
![AB=\left[\begin{array}{cc}a_(11)b_(11)+a_(12)b_(21)&a_(11)b_(12)+a_(12)b_(22)\\a_(21)b_(11)+a_(22)b_(21)&a_(21)b_(12)+a_(22)b_(22)\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/122wmkzfaybg6920vtgq7hmipqfq06gej1.png)
IMPORTANT: It's not the same AB then BA the results of both products are differents.
Now we are going to analyze every option:
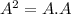
Option 1:
![A=\left[\begin{array}{cc}5&5\\-4&-4\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/3ve3cbvri7xwsb0cp737ng02djxoxtiowe.png)
![A.A=\left[\begin{array}{cc}5&5\\-4&-4\end{array}\right] .\left[\begin{array}{cc}5&5\\-4&-4\end{array}\right] =\\\\=\left[\begin{array}{cc}5.5+5(-4)&5.5+5(-4)\\(-4).5+(-4).(-4)&(-4).5+(-4)(-4)\end{array}\right] \\\\=\left[\begin{array}{cc}25-20&25-20\\-20+16&-20+16\end{array}\right] \\\\=\left[\begin{array}{cc}5&5\\-4&-4\end{array}\right]=A](https://img.qammunity.org/2019/formulas/mathematics/high-school/2n0gasr6ok2abttookl60ayrzmi8mkn1mo.png)
We can see that A.A=A then this is the correct option.
Option 2:
![A=\left[\begin{array}{cc}6&5\\5&6\end{array}\right]\\\\A.A=\left[\begin{array}{cc}6&5\\5&6\end{array}\right].\left[\begin{array}{cc}6&5\\5&6\end{array}\right]\\\\=\left[\begin{array}{cc}6.6+5.5&6.5+5.6\\5.6+6.5&5.5+6.6\end{array}\right]\\\\=\left[\begin{array}{cc}36+25&30+30\\30+30&25+36\end{array}\right]\\\\=\left[\begin{array}{cc}61&60\\60&61\end{array}\right]\\eq A](https://img.qammunity.org/2019/formulas/mathematics/high-school/1mcsft9iamv0rxbhyrvtp5swnog3m0dhny.png)
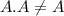 Then this option is incorrect.
Then this option is incorrect.
Option 3:
![A=\left[\begin{array}{cc}0,5&-0,5\\-0,5&0,5\end{array}\right] \\\\A.A=\left[\begin{array}{cc}0,5&-0,5\\-0,5&0,5\end{array}\right].\left[\begin{array}{cc}0,5&-0,5\\-0,5&0,5\end{array}\right]\\\\=\left[\begin{array}{cc}0,5.0,5+(-0,5).(-0,5)&0,5.(-0,5)+(-0,5).(0,5)\\(-0,5).0,5+0,5.(-0,5)&(-0,5).(-0,5)+0,5.0,5\end{array}\right]\\\\=\left[\begin{array}{cc}0,25+0,25&-0,25-0,25\\-0,25-0,25&0,25+0,25\end{array}\right]\\\\=\left[\begin{array}{cc}0,5&-0,5\\-0,5&0,5\end{array}\right]= A](https://img.qammunity.org/2019/formulas/mathematics/high-school/9ek89621yiacnu7105nv4rprj7ebbfupn0.png)
We can see that this option is also correct.
Option 4:
![A=\left[\begin{array}{cc}0,5&0,5\\-0,5&0,5\end{array}\right] \\\\A.A=\left[\begin{array}{cc}0,5&0,5\\-0,5&0,5\end{array}\right].\left[\begin{array}{cc}0,5&0,5\\-0,5&0,5\end{array}\right]\\\\=\left[\begin{array}{cc}0,5.0,5+0,5.(-0,5)&0,5.0,5+0,5.0,5\\(-0,5).0,5+0,5.(-0,5)&(-0,5).0,5+0,5.0,5\end{array}\right]\\\\=\left[\begin{array}{cc}0,25-0,25&0,25+0,25\\-0,25-0,25&-0,25+0,25\end{array}\right]\\\\=\left[\begin{array}{cc}0&0,5\\-0,5&0\end{array}\right]\\eq A](https://img.qammunity.org/2019/formulas/mathematics/high-school/qypzi9ft0anctw4iaaplucz6wj2ogwypoz.png)
Then this option is incorrect.
Option 5:
![A=\left[\begin{array}{cc}-6&-6\\5&5\end{array}\right]\\\\A.A=\left[\begin{array}{cc}-6&-6\\5&5\end{array}\right].\left[\begin{array}{cc}-6&-6\\5&5\end{array}\right]\\\\=\left[\begin{array}{cc}(-6).(-6)+(-6).5&(-6).(-6)+(-6).5\\5.(-6)+5.5&5.(-6)+5.5\end{array}\right]\\\\=\left[\begin{array}{cc}36-30&36-30\\-30+25&-30+25\end{array}\right]\\\\=\left[\begin{array}{cc}6&6\\-5&-5\end{array}\right]\\eq A](https://img.qammunity.org/2019/formulas/mathematics/high-school/qe589ukpdttl4kugfv68pd8wy07xyhns9v.png)
Then this option is incorrect.