Question

Question 3 Unsaved Solve for x, given the equation Square root of x minus 5 + 7 = 11

Answer 1

We have the following equation:

`√(x-5) +7=11`

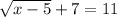
To solve this, we first need to subtract the 7 on both sides of the equation.

`√(x-5) +7-7=11-7`

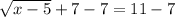
The equation then becomes:

`√(x-5) =4`

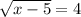
Now we must square both sides of the equation to get rid of the radical/square root symbol.

`(√(x-5))^2 =(4)^2`

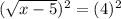
Now we have a normal one step equation.

`x-5=16`

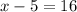
Add 5 on both sides to find x.

`x-5+5=16+5`

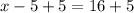
x=21

To see if this solution is true, we must substitute 21 back into the original equation.

`√(21-5) +7=11`

`√(16) +7=11`

`4+7=11`

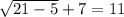
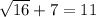
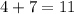
11=11

Therefore, the solution is true.

Answer 2

`Domain:\\\\x-5\geq0\to x\geq5\\\\√(x-5)+7=11\ \ \ \ \ |-7\\\\√(x-5)=4\ \ \ \ \ |^2\\\\(√(x-5))^2=4^2\to x-5=16\ \ \ \ \ |+5\\\\\boxed{x=21}\in D\\\\`