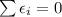Answer:
Properties of Fitted Regression Line
Explanation:
We know that,
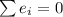
In turn we understand that
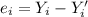
The third property of Fitted Regression Line tells us that: The sum of the observed values
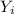 equals the sum of the fitted values
equals the sum of the fitted values
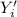 , so:
, so:
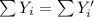 (1)
(1)
We further understand that the values given for
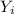 , is equivalent to:
, is equivalent to:
 (2)
(2)
On the other hand for the definition of the value for the regression function of
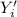 is,
is,
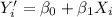 (3)
(3)
By replacing (3) and (2) in (1), we get that

Since the sum is distributive
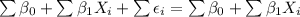
Equal values on opposite sides of an equation are canceled, we get that