2 Answers

Johnildergleidisson · Answer 1 · 2019-10-09T04:03:06+0000

The sum of logs is the log of the product.

Law of logarithms:

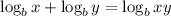
$\log_b x + \log_b y = \log_b xy$

Apply the law above to the left side of the equation.

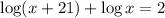
$\log (x + 21) + \log x = 2$

$\log [x(x + 21)] = 2$

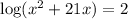
$\log (x^2 + 21x) = 2$

Now use the definition of log.

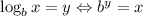
$\log_b x = y \Leftrightarrow b^y = x$

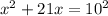
x^2 + 21x = 10^2

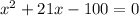
x^2 + 21x - 100 = 0

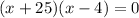
(x + 25)(x - 4) = 0

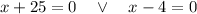
$x + 25 = 0~~~\lor~~~x - 4 = 0$

$x = -21~~~\lor ~~~x = 4$

x = -21 must be discarded because log (x + 21) would become log (-21) which is not defined.

Solution: x = 4

Please log in or register to add a comment.