The sum of logs is the log of the product.
Law of logarithms:
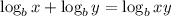
Apply the law above to the left side of the equation.
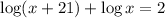
![\log [x(x + 21)] = 2](https://img.qammunity.org/2019/formulas/mathematics/middle-school/l9dvhnqjjlooorp263q9dz8en954ubvyom.png)
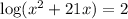
Now use the definition of log.
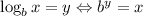
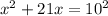
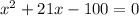

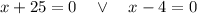

x = -21 must be discarded because log (x + 21) would become log (-21) which is not defined.
Solution: x = 4