Question

Which is a counterexample for the conditional statement? If a square has side length s, then the perimeter is less than the area. s = 3 s = 5 s = 7 s = 9

Answer 1

s=3. the perimeter, 12, is greater than the area, 9

Answer 2

Side length s = 3 is the counter-example for the given statement.

Explanation:

We are given that the side length of a square = s.

Now, we know that,

Perimeter of a square =
`4s`

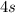
Area of a square =
`s^2`

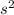
Then, the table showing the perimeter and area of a square for different side length is given by,

Side length (s) Perimeter =
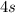`4s` Area =
`s^2`

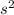
3 12 9

5 20 25

7 28 49

9 36 81

Now, we need a counter-example for the statement,

'If the side length of a square is 's', then the perimeter is less than the area'.

From the table, we see that,

When the side length of the square is 3, then perimeter = 12 > 9 = area.

Thus, side length s = 3 is the counter-example for the given statement.