The plus-minus sign represents that there are two possible outcomes.
In this case, we have

. When we branch out the possibilities we got 2 values:

and
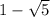
Those are the roots of this equation. When they ask their product, they want you to multiply both numbers.
When we multiply them:

When we FOIL the we get:

Simplify:
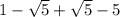
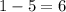
So the product of the two roots of this equation is 6.