Use factorials to solve this problem.
When you are choosing a number of digits from a set without repetition, you will use the following formula:
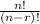
n represents the total amount of items in the set, and r represents the number of items you will take out.
There are 10 digits, and you are choosing sets of 6 digits for your code. Plug the values into the equation:
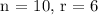
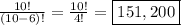
There are
151,200 different 6-digit codes possible.