Question

Your answer is incorrect. Suppose that a "code" consists of 6 digits, none of which is repeated. (A digit is one of the 10 numbers 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .) How many codes are possible?

Answer 1

Use factorials to solve this problem.

When you are choosing a number of digits from a set without repetition, you will use the following formula:


`(n!)/((n-r)!)`

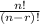
n represents the total amount of items in the set, and r represents the number of items you will take out.

There are 10 digits, and you are choosing sets of 6 digits for your code. Plug the values into the equation:


`\text{n = 10, r = 6}`


`(10!)/((10-6)!) = (10!)/(4!) = \boxed{151,200}`

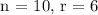
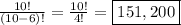
There are 151,200 different 6-digit codes possible.

Answer 2

take me the brayniest.i hope it was helpful