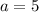The Law of Cosines is a beautiful formula and a gateway to all sorts of wonders.
This question asking for the length to the nearest whole number is pretty ugly.
A diagonal of a parallelogram makes two congruent triangles. In this problem we're almost told we're interested in the diagonal opposite an A=55 degree angle, included between sides b=4 and c=6.

We just plug in the numbers.
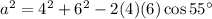
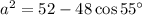
That's the exact answer, its square anyway. Now we approximate.
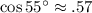
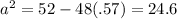
Taking the square root to the nearest integer,