Question

Misha found that the equation -|2x-10|-1=2 had two possible solution x=3.5and x =-6.5. Which explains whether or not her solutions are correct

Answer 1

-|2x-10|-1=2 has NO solutions, because the absolute value function is never negative. Can be 0, can be positive, but can NOT be negative.

Answer 2

She is not correct.

Explanation:

Given : Misha found that the equation
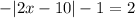`- |2x-10|-1=2` had two possible solution x=3.5 and x =-6.5.

To find : Explains whether or not her solutions are correct.

Solution :

The first thing we solve the equation to get solution,

`- |2x-10|-1=2`

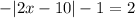
Add 1 on both side of equation :

`- |2x-10|-1+1=2+1`

`- |2x-10|=3`

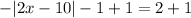
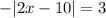
Multiply both sides of the equation by -1:

`- |2x-10|(-1)=3(-1)`

`|2x-10|=-3`

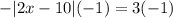
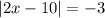
We observe that the result of the expression in absolute value is -3.

The result of an absolute value function is always greater than or equal to zero.

Which implies , the equation has no solution.

Therefore, Misha solutions were incorrect.