Answer:
She is not correct.
Explanation:
Given : Misha found that the equation
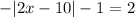 had two possible solution x=3.5 and x =-6.5.
had two possible solution x=3.5 and x =-6.5.
To find : Explains whether or not her solutions are correct.
Solution :
The first thing we solve the equation to get solution,
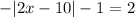
Add 1 on both side of equation :
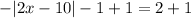
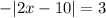
Multiply both sides of the equation by -1:
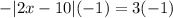
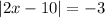
We observe that the result of the expression in absolute value is -3.
The result of an absolute value function is always greater than or equal to zero.
Which implies , the equation has no solution.
Therefore, Misha solutions were incorrect.