Question

Triangle ABC has vertices at A(–2, 3), B(–3, –6), and C(2, –1). Is triangle ABC a right triangle? If so, which angle is the right angle?

Answer 1

B. A’(3, –2), B’(3, –5), C’(2, –4)

Explanation:

Got it right on Edge :)

Answer 2

We'll use rise over run to find the slopes of two of the sides of the triangle:


`(y_(2) - y_(1))/(x_(2) - x_(1))`

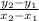
Because C is the rightmost point, we'll have it represent (x1,y1), and have A and B represent (x2,y2):

A to C
(-2,3) to (2,-1)


`(-1 - 3)/(2 + 2) = (-4)/(4) = -1`

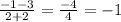
The slope of the line from A to C is -1.

B to C
(-3,-6) to (2,-1)


`(-1 + 6)/(2+3) = (5)/(5) = 1`

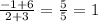
The slope of the line from B to C is 1.

These lines intersect at (2,-1), and they have negative reciprocal slopes of each other, which creates a perpendicular angle. This means that triangle ABC is a right triangle, and angle ACB is the right angle.