In order to do this you have to put it into vertex form, which is achieved by completing the square. Start out by setting it equal to 0.
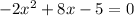
. Next, move the 5 over to the other side of the equals sign.
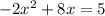
. In order to complete the square, the rule is that the leading coefficient on the squared term is a positive 1. Ours is a -2, so we have to factor it out.

. Complete the square by taking half the linear term (the linear term is 4 now), square it and add it to both sides. Half of 4 is 2, and 2 squared is 4, so we will add it in. HOWEVER, when you add it into the parenthesis on the left, you still have that -2 hanging out front, so what you really have added in is -2(4) which is -8. Here's what we have now so far:
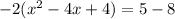
which simplifies to
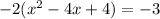
. The next step is to create the perfect square binomial we formed during this process on the left, which gives us
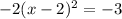
. Move the -3 back over to the other side by addition and you get
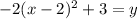
. This tells us that our vertex is (2, 3)