Question

3. When two atoms of 2H (deuterium) are fused to form one atom of 4He (helium), the total energy evolved is 3.83 × 10-12 joules. What is the total change in mass (in kilograms) for this reaction?

4. The mass of a proton is 1.00728 atomic mass units (amu) and the mass of a neutron is
60Co nucleus whose nuclear mass is 1.00867 amu. What is the mass defect (in amu) of a 27
59.9338 amu? What is the mass defect in kilograms? What is the energy equivalent of this mass in kilojoules?
5. The equation shows one mole of ethanol fuel being burned in oxygen. Convert the energy released into its equivalent mass.
C2H5OH(l) + 3 O2(g)  2 CO2(g) + 3 H2O (l) ΔH = -1418 kJ/mol

Answer 1

3.
∆E = ∆m x c ² ∆m = E / c ² ∆m = 3,83•10^-12 / 3•10^8 ² ∆m = 4,256•10^-29 kg

Taking this class as well

Answer 2

For 3: The total mass change of the reaction is
`4.255* 10^(3)kg`

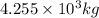
For 4: The mass defect is
`0.911* 10^(-27)kg` and energy equivalent to this mass is
`8.199* 10^(-14)kJ`

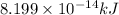
For 5: The equivalent mass of the reaction is
`1.5755* 10^(-11)kg`

Step-by-step explanation:

• For 3:

To calculate the mass change of the reaction for given energy released, we use Einstein's equation:

`E=\Delta mc^2`

E = Energy released =
`3.83* 10^(-12)J`

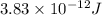
`\Delta m` = mass change = ?

c = speed of light =
`3* 10^8m/s`

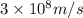
Putting values in above equation, we get:

`3.83* 10^(-12)Kgm^2/s^2=\Delta m* (3* 10^8m/s)^2\\\\\Delta m=4.255* 10^3kg`

Hence, the total mass change of the reaction is
`4.255* 10^(3)kg`

• For 4:

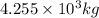
For the given isotopic representation:
`_(27)^(60)\textrm{Co}`

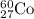
Atomic number = Number of protons = 27

Mass number = 60

Number of neutrons = Mass number - Atomic number = 60 - 27 = 33

To calculate the mass defect of the nucleus, we use the equation:

`\Delta m=[(n_p* m_p)+(n_n* m_n)+]-M`

where,

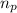`n_p` = number of protons = 27

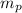`m_p` = mass of one proton = 1.00728 amu

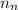`n_n` = number of neutrons = 33

`m_n` = mass of one neutron = 1.00867 amu

M = Nuclear mass number = 59.9338 amu

Putting values in above equation, we get:

`\Delta m=[(27* 1.00728)+(33* 1.00867)]-[59.9338]\\\\\Delta m=0.54887amu`

Converting the value of amu into kilograms, we use the conversion factor:

`1amu=1.66* 10^(-27)kg`

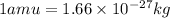
So,
`0.54887amu=0.54887* 1.66* 10^(-27)kg=0.911* 10^(-27)kg`

To calculate the equivalent energy, we use the equation:

`E=\Delta mc^2`

E = Energy released = ?

`\Delta m` = mass change =
`0.911* 10^(-27)kg`

c = speed of light =
`3* 10^8m/s`

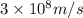
Putting values in above equation, we get:

`E=(0.911* 10^(-27)kg)* (3* 10^8m/s)^2\\\\E=8.199* 10^(-11)J`

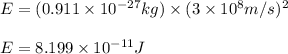
Converting this into kilojoules, we use the conversion factor:

1 kJ = 1000 J

So,
`8.199* 10^(-11)J=8.199* 10^(-14)kJ`

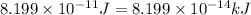
Hence, the mass defect is
`0.911* 10^(-27)kg` and energy equivalent to this mass is
`8.199* 10^(-14)kJ`

• For 5:

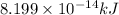
For the given chemical reaction:

`C_2H_5OH(l)+3O_2(g)\rightarrow 2CO_2(g)+3H_2O(l);\Delta H=-1418kJ/mol`

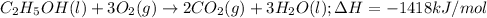
To calculate the equivalent mass of the reaction for given energy released, we use Einstein's equation:

`E=\Delta mc^2`

E = Energy released =
`1418kJ=1418* 10^3J`

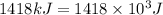
`\Delta m` = mass change = ?

c = speed of light =
`3* 10^8m/s`

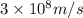
Putting values in above equation, we get:

`1418* 10^(3)Kgm^2/s^2=\Delta m* (3* 10^8m/s)^2\\\\\Delta m=1.5755* 10^(-11)kg`

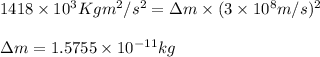
Hence, the equivalent mass of the reaction is
`1.5755* 10^(-11)kg`