Answer:
The "tallest truck" that it passes by is 12 ft.
Step-by-step explanation:
Given that,
The truck passes through "Height of an half ellipse" is 20 ft ("a" is "Major axis").
The truck passes through "Width of an ellipse" is 20 ft ("b" is "Minor axis").
The width of the truck is 16 ft (x).
We need to find the greatest "height of the truck" (y) which enters into an ellipse.
We know that,
Equation of ellipse is
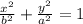
Substitute the given values in the above formula,
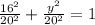
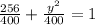

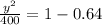
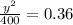
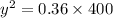
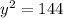
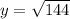
y = 12
Therefore, The "tallest truck" that it passes by is 12 ft.