Question

Choose the true statement about the graph of 3x > 6

A.) Open circle on 2 and all the numbers to the left are shaded

B.) Open circle on 2 and all the numbers to the right are shaded

C.) Closed circle on 2 and all the numbers to the right are shaded

D.) Closed circle on 2 and all the numbers to the left are shaded

Answer 1

B

Explanation:

Given

3x > 6 ( divide both sides by 3 )

x > 2

> is denoted by an open circle at 2 on the number line, meaning that x cannot equal 2. Since values are greater than 2 then numbers to the right of 2 are shaded.

This would be represented by graph B

Answer 2

Answer: B.) Open circle on 2 and all the numbers to the right are shaded

Explanation:

The given inequality :
`3x>6`

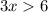
Divide both sides by 3 , we get

`x>2`

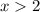
i.e. x is a numerical value strictly greater than 2 i.e. 2 is not-included.

When we plot this inequality on Number line , we starts with an open circle on 2 that signifies that 2 in not included and shade on the right side because x is greater than 2 which lies on the right side of 2 .

Hence, the correct answer is B.) Open circle on 2 and all the numbers to the right are shaded .