Question

A fighter plane flying at constant speed 420 m/s and constant altitude 3300 m makes a turn of curvature radius 11000 m. On the ground, the plane’s pilot weighs (53 kg) (9.8 m/s 2 ) = 519.4 N. What is his/her apparent weight during the plane’s turn? Answer in units of N

Answer 1

518.86 N

Step-by-step explanation:

mass of pilot, m = 53 kg

g = 9.8 m/s^2

h = 3300 m

Radius of earth, R = 6378.1 km

Let the value of acceleration due to gravity at a height is g'.

`g'=g\left ( 1-(2h)/(R) \right )`

`g'=g\left ( 1-(2* 3300)/(6378.1 * 1000) \right )`

g' = 9.7898 m/s^2

Weight of pilot

W' = m x g' = 53 x 9.7898 = 518.86 N

Answer 2

"Apparent weight during the "plan's turn" is 519.4 N

Step-by-step explanation:

The "plane’s altitude" is not so important, but the fact that it is constant tells us that the plane moves in a "horizontal plane" and its "normal acceleration" is
`\mathrm{a}_{\mathrm{n}}=(v^(2))/(R)`

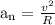
Given that,

v = 420 m/s

R = 11000 m

Substitute the values in the above equation,

`a_(n)=(420^(2))/(11000)`

`a_(n)=(176400)/(11000)`

`a_(n)=16.03 \mathrm{m} / \mathrm{s}^(2)`

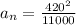
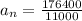
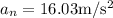
It has a horizontal direction. Furthermore, constant speed implies zero tangential acceleration, hence vector a = vector a N. The "apparent weight" of the pilot adds his "true weight" "m" "vector" "g" and the "inertial force""-m" vector a due to plane’s acceleration, vector
`W_{\mathrm{app}}=m(\text { vector } g \text { -vector a })`

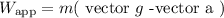
In magnitude,

`| \text { vector } g-\text { vector } a |=\sqrt{\left(g^(2)+a^(2)\right)}`

`| \text { vector } \mathrm{g}-\text { vector } \mathrm{a} |=\sqrt{\left(9.8^(2)+16.03^(2)\right)}`

`| \text { vector } \mathrm{g}-\text { vector } \mathrm{a} |=√((96.04+256.96))`

`| \text { vector } \mathrm{g}-\text { vector } \mathrm{a} |=√(353)`

`| \text { vector } \mathrm{g}-\text { vector } \mathrm{a} |=18.78 \mathrm{m} / \mathrm{s}^(2)`

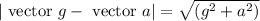
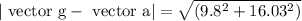
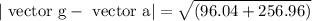
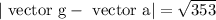
Because vector “a” is horizontal while vector g is vertical. Consequently, the pilot’s apparent weight is vector

`\mathrm{W}_{\mathrm{app}}=(18.78 \mathrm{m} / \mathrm{s}^ 2)(53 \mathrm{kg})=995.77 \mathrm{N}`

Which is quite heavier than his/her true weigh of 519.4 N