Answer:
"Apparent weight during the "plan's turn" is 519.4 N
Step-by-step explanation:
The "plane’s altitude" is not so important, but the fact that it is constant tells us that the plane moves in a "horizontal plane" and its "normal acceleration" is
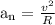
Given that,
v = 420 m/s
R = 11000 m
Substitute the values in the above equation,
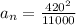
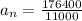
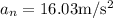
It has a horizontal direction. Furthermore, constant speed implies zero tangential acceleration, hence vector a = vector a N. The "apparent weight" of the pilot adds his "true weight" "m" "vector" "g" and the "inertial force""-m" vector a due to plane’s acceleration, vector
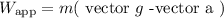
In magnitude,
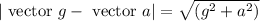
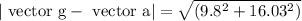
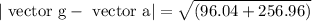
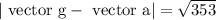
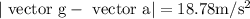
Because vector “a” is horizontal while vector g is vertical. Consequently, the pilot’s apparent weight is vector
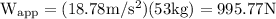
Which is quite heavier than his/her true weigh of 519.4 N