Answer:
a) PMT=$1,213.86 ; b) Total interest = $67,494.80
Explanation:
a) In order to find their monthly payment we must start by determining the amount to be borrowed.
$191,000-$40,000=$151,000
Once we got this amount, we can make use of the annuity formula to fin the monthly payment:
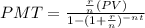
Where
PMT = monthly payment.
r = interest rate written as a decimal number.
n = number of times the interest will be compounded in a year.
PV = present value of the loan.
t = number of years.
So we know the following data:
r = 0.0525
n = 12
PV = $151,000
t = 15
So we can plug those numbers into the formula, so we get:
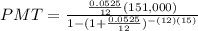
which solves to:
PMT=$1,213.86
b)
In order to find the interest they paid over the entire loan we must first find how much they paid in total for the loan. So we get the monthly payment and multiply that by the total number of months so we get:
Total=$1,213.86*12*15=$218,494.80
next, we subtract the original amount of the loan from that to determine how much of it is interest:
Total interest = $218,494.80-$151,000=$67,494.80