Question

69 points!!!

What are the solutions of the following system?
{x² + y² = 25
{ 2x+y=-5

A(0,-5) and (-5,5)
B (0,-5) and (5, -15)
C(0, -5) and (-4,3)
D(0,-5) and (4, -13)

Answer 1

C.

Explanation:

on edge 2020 :))

Answer 2

C) The solution for the given system of equations are A(0,-5) and B(-4,3)

Explanation:

The given system of equation are :
`x^(2)  + y^(2)  = 25\\2x  + y  = -5`

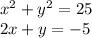
from equation 2, we get y = -5 - 2x .

Put the above value of y in the equation (1).

We get:
`x^(2)  + y^(2)  = 25  \implies x^(2)  + (-5-2x)^(2)  = 25`

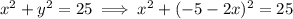
By ALGEBRAIC IDENTITY:

`(a+b)^(2)   = a^(2)  +  b^(2)  + 2ab\\ (-5-2x)^(2) = (-5)^(2)  +  (-2x)^(2)  + 2(-5)(-2x)`

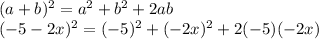
or,
`x^(2)  + (-5-2x)^(2)  = 25  \implies x^(2) + (25  +  4x^(2)  + 20x)  = 25`

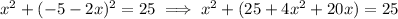
or,
`5x^(2)  + 20x = 0  \implies x(5x + 20) = 0`

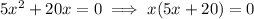
⇒ x = 0 or, x = -20/5 = -4

So, the possible values for x are: x = 0 or x = -4

If x = 0, y = -5-2x = -5-2(0) = -5

and if x = -4, y = -5 -2(-4) = -5 + 8 = 3

Hence, the solution for the given system of equations are A(0,-5) and B(-4,3)