Answer:
C) The solution for the given system of equations are A(0,-5) and B(-4,3)
Explanation:
The given system of equation are :
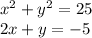
from equation 2, we get y = -5 - 2x .
Put the above value of y in the equation (1).
We get:
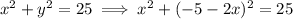
By ALGEBRAIC IDENTITY:
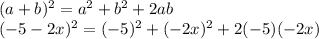
or,
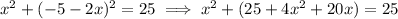
or,
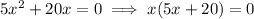
⇒ x = 0 or, x = -20/5 = -4
So, the possible values for x are: x = 0 or x = -4
If x = 0, y = -5-2x = -5-2(0) = -5
and if x = -4, y = -5 -2(-4) = -5 + 8 = 3
Hence, the solution for the given system of equations are A(0,-5) and B(-4,3)