Answer:
Length of the side AC is 12 units.
Explanation:
Here, in the triangle ABC
Base = 5 units
Let, Perpendicular = k units
Hypotenuse = 13 units
In a Right angle triangle, by PYTHAGORAS THEOREM:
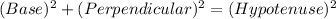
Similarly, in triangle ABC
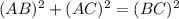
or,
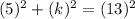
⇒
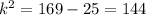
⇒ k = 12, or k= -12
But as k is the length of a side of a triangle so, k ≠ -12
⇒ k = 12
Hence, the length of the side AC = 12 units.