Question

Calculate the length of AC​

Answer 1

By applying Pythagorean theorem to right-angled triangle ABC, the length of segment AC is equal to 12 units.

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

In order to determine the length of segment AC, we would have to apply Pythagorean theorem to right-angled triangle ABC as follows;

`AC^2 = CB^2 - AB^2\\ \\AC^2 = 13^2 - 5^2\\\\AC^2 = 169-25\\\\AC^2 = 144\\\\AC=√(144)`

AC = 12 units.

Answer 2

Length of the side AC is 12 units.

Explanation:

Here, in the triangle ABC

Base = 5 units

Let, Perpendicular = k units

Hypotenuse = 13 units

In a Right angle triangle, by PYTHAGORAS THEOREM:

`(Base)^(2)  + (Perpendicular)^(2)  =  (Hypotenuse)^(2)`

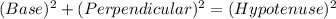
Similarly, in triangle ABC

`(AB)^(2)  + (AC)^(2)  =  (BC)^(2)`

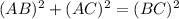
or,
`(5)^(2)  + (k)^(2)  =  (13)^(2)`

⇒
`k^(2)  = 169 - 25 = 144`

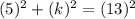
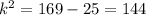
⇒ k = 12, or k= -12

But as k is the length of a side of a triangle so, k ≠ -12

⇒ k = 12

Hence, the length of the side AC = 12 units.