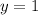Question

Solve the system of equations by substitution. x + y = A system of equations. StartFraction 3 over 8 EndFraction x plus StartFraction one-third EndFraction y equals StartFractions 17 over 24 EndFraction. x + 7y = 8 ( , )

Answer 1

(1,1)

Explanation:

juss took it

Answer 2

`x=1` and
`y=1`

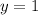
Explanation:

We have to solve by substitution the given system of equations:

`\left \{ {{(3)/(8)x+(1)/(3)y=(17)/(24) }\atop {x+7y=8}} \right.`

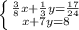
First, we have to choose an equation, no matter which one, and isolate a certain variable, no matter which one either. So, by our own criteria, we choose the second equation, and we'll isolate x:

`x+7y=8\\x=8-7y`

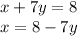
Now, this equivalence for x, we will replace it in the other equation, instead of x, we will put the result:

`(3)/(8)(8-7y)+(1)/(3)y=(17)/(24)`

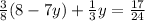
Then, we solve for y:

`(3)/(8)(8-7y)+(1)/(3)y=(17)/(24)\\(3)/(8)8-(3)/(8)7y+(1)/(3)y=(17)/(24)\\-(21)/(8)y+(1)/(3)y=(17)/(24)-3\\(-63y+8y)/(24)=(17-72)/(24)\\ (-55y)/(24)=(-55)/(24)\\y=(-55(24))/(24(-55))=1`

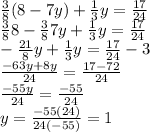
Now, the final process will be to replace this y-value in one equation, no matter which one, and find x-value:

`x+7y=8\\\\x+7(1)=8\\x=8-7\\x=1`

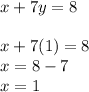
Therefore, the solution of the system is
`x=1` and
`y=1`