Answer:
The value of x and y is 9 and 4 units
Solution:
We have,
DH = x+3; HF= 3y and GH=3x-3; HE =5y + 4
For parallelogram, we know that,
DH=HF
So,
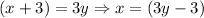 --------- (i)
--------- (i)
Again, GH = HE
So,
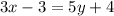
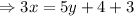
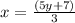 ………. (ii)
………. (ii)
Now equating both (i) and (ii) we get,
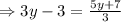
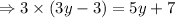
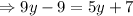
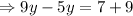
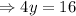
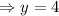
So the value of
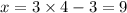
The value of x and y is 9 and 4 units