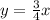Answer:
The equation of the line passing through (0,0) and (4,3) is
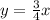
Solution:
Given pair of points are (0,0) and (4,3)
Here,
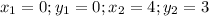
We know the slope of an equation is given by y = mx+c
Where “m” is the slope of the line and “c” is the y-intercept
To find the value of m, we use the below given formula
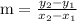
Substituting the values we get,
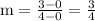
Putting the value of m in the slope intercept form we get,
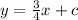
To find the value of c, we substitute the value of x and y from any two given point. Lets take x = 4 and y = 3
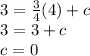
Therefore the slope intercept equation becomes